Lambertian reflectance
If a surface exhibits Lambertian reflectance, light falling on it is scattered such that the apparent brightness of the surface to an observer is the same regardless of the observer's angle of view. More technically, the surface luminance is isotropic. For example, unfinished wood exhibits roughly Lambertian reflectance, but wood finished with a glossy coat of polyurethane does not, since specular highlights may appear at different locations on the surface. Not all rough surfaces are perfect Lambertian reflectors, but this is often a good approximation when the characteristics of the surface are unknown. Lambertian reflectance is named after Johann Heinrich Lambert.
Contents |
Use in computer graphics
In computer graphics, Lambertian reflection is often used as a model for diffuse reflection. This technique causes all closed polygons (such as a triangle within a 3D mesh) to reflect light equally in all directions when rendered. In effect, a point rotated around its normal vector will not change the way it reflects light. However, the point will change the way it reflects light if it is tilted away from its initial normal vector.[1] The reflection is calculated by taking the dot product of the surface's normal vector, 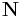 , and a normalized light-direction vector,
, and a normalized light-direction vector, 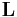 , pointing from the surface to the light source. This number is then multiplied by the color of the surface and the intensity of the light hitting the surface:
, pointing from the surface to the light source. This number is then multiplied by the color of the surface and the intensity of the light hitting the surface:
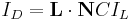 ,
,
where  is the intensity of the diffusely reflected light (surface brightness),
is the intensity of the diffusely reflected light (surface brightness),  is the color and
is the color and  is the intensity of the incoming light. Because
is the intensity of the incoming light. Because
 ,
,
where  is the angle between the direction of the two vectors, the intensity will be the highest if the normal vector points in the same direction as the light vector (
is the angle between the direction of the two vectors, the intensity will be the highest if the normal vector points in the same direction as the light vector ( , the surface will be perpendicular to the direction of the light), and the lowest if the normal vector is perpendicular to the light vector (
, the surface will be perpendicular to the direction of the light), and the lowest if the normal vector is perpendicular to the light vector ( , the surface runs parallel with the direction of the light).
, the surface runs parallel with the direction of the light).
Lambertian reflection from polished surfaces are typically accompanied by specular reflection (gloss), where the surface luminance is highest when the observer is situated at the perfect reflection direction (i.e. where the direction of the reflected light is a reflection of the direction of the incident light in the surface), and falls off sharply. This is simulated in computer graphics with various specular reflection models such as Phong, Cook-Torrance. etc.
Spectralon is a material which is designed to exhibit an almost perfect Lambertian reflectance, while Scotchlite is a material designed with the opposite intent of only reflecting light on one line of sight.
Other waves
While Lambertian reflectance usually refers to the reflection of light by an object, it can be used to refer to the reflection of any wave. For example, in ultrasound imaging, "rough" tissues are said to exhibit Lambertian reflectance.
See also
References
- ^ Angel, Edward (2003). Interactive Computer Graphics: A Top-Down Approach Using OpenGL (third ed.). Addison-Wesley. ISBN 978-0-321-31252-5. http://books.google.com/?id=Fsy_QgAACAAJ.